Physics Puzzler: Dunk Tank Physics

A dunking booth, or dunk tank, is a simple machine that’s usually set up outside. A person sits on a board suspended above a large container of water. The board is held in place by a latch. Passersby purchase the chance to throw a ball at a target that’s connected to the latch—hit the target and the latch gives, dropping the person straight into the chilly water below. Then rinse and repeat.

Anyone with experience can attest to how unpleasant it can be to sit above the tank. Not just because it’s nerve-wracking, but also because it gets so cold! But, is it really that cold up there? Does it even matter how many times you get dunked?
To answer this, we need not only thermal physics but also some fluid dynamics that to this day has not been solved completely. So, I challenge you to puzzle out:

How much energy does a dunked person need to keep warm?

This is a complicated problem, so consider a related question. If you were sitting in a dunk tank for an hour, would you prefer being dunked just once and slowly drying off or being plunged into the water continuously? Which has a greater cooling power?

Let’s look at each case.

When you’re plunged into the water for the first time, you get completely submerged. If the water were the same temperature as a human, 37 °C, you might not mind too much, but heated dunk tanks aren’t really a thing. Groundwater temperatures are fairly constant throughout the year, so if the tank were just filled, it would probably be a little chilly.¹ The temperature varies with location and latitude, 5 °C – 25 °C being a fair range, so we’ll pick the value for Washington, DC: 11 °C (53 °F). That’s pretty cold! Also remember that water can absorb and store a lot of energy per degree change, a fact reflected in its high specific heat:

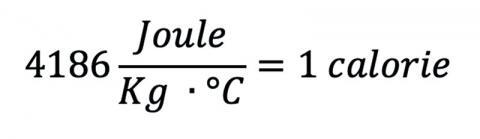
which is significantly higher than that of steel (420 J/kg °C), wood (1760 J/kg °C), or even sand (830 J/kg °C).² Very few common materials have a higher specific heat.

From introductory physics, we can calculate the heat flow between two materials:

where Q is the heat flow, m is the mass of the material in question, c is the object’s specific heat (material dependent), and ΔT is the material’s temperature change from TI to TF. Given enough time, two materials with arbitrary mass and specific heats in thermal contact will eventually reach a thermal equilibrium if they start at different temperatures T1 and T2, assuming no additional heat sources and a closed system. This gives us

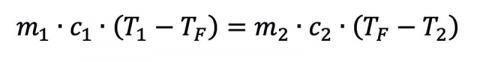
where the superscripts reference the different initial conditions. If a person was dunked and stayed in the water (or was dunked a lot), we could even solve for the final temperature:

but this process would take a long time, and most people are in the water for only a few seconds. Since humans are mostly water and have a volume on the order of 70 L, the 800 L (200 gallons) of cold water won’t warm up very much with repeated dunks, but the person will relatively cool down more and more each time. What would the final temperature be? Luckily, people can last for long periods in the cold water well before they get too cold, because the human body generates a lot of heat and stays at about the same temperature!

Now let’s come up with an order-of-magnitude estimate. Note your answer; we’ll need it later.

If the water and person did come to thermal equilibrium and it took about an hour (much less than a day but more than a few minutes), how many kJ would the human body have contributed to make up the difference?⁴

Now recall our thought experiment: Would you get colder sitting on the dunk tank board drying off or being repeatedly dunked? To answer that, we need to consider what happens after you get out of the dunk tank.

To simplify the problem, let’s assume it’s a very slow day at the dunk tank and the person getting dunked gets dropped only once and that it’s at the start of the hour. When you climb out, you’re coated in in about ¹ L of water thanks to your clothes and hair. Let’s assume that after an hour you’re bone dry, this time thanks to evaporative cooling³. While your body will radiate heat through black body radiation, conduct heat onto surrounding matter, and lose heat through convection (motion of air around your skin), evaporation of water is most likely the primary way you’ll lose heat to the surrounding environment. Just as if it’s a very hot day, taking a quick dip in a pool or even sweating causes people to cool off quickly. On very hot occasions, people can sweat well over 1 L per hour!⁵

The amount of energy you’ll lose as 1 L of water evaporates at room temperature can be measured using the heat capacity and the heat of vaporization for water. It turns out to be about 2400 kJ/kg at room temperature.6 Thus, if someone had 1 L of water coating them (about 1 kg) and it evaporated, the water would need about 2400 kJ of energy to vaporize. While this isn’t the only cooling process, it’s fair to consider this a lower limit because radiation, conduction, and convection will cool you even more. That’s a lot of energy . . .

Comparing the energy you’d lose by warming the water for an hour with the energy you’d lose by evaporation over an hour, we can see that they are order-of-magnitude comparable. While neither case includes lots of details, both processes are cooling the person in the dunk tank considerably! We’d need better models to determine which situation would actually cool you faster, but I would argue that whether you are being put in the water continuously or just once, both sound like pretty unpleasant experiences on all but the hottest days of the year.

This line of reasoning raises another question that we’ll leave you to reason through. A person falling into cool water will add gravitational energy, which is then transferred into thermal energy through complicated turbulence processes, thereby heating the water. The person will also warm the water for every unit of time they are submerged.

How many dunks would it take to measurably increase the temperature of the water?

A “Physics Dunk Tank” Physics Problem

A fun physics edition of the dunk tank game might involve throwing a ball that hits a lever and releases another lever that holds up the seat. There are lots of physics principles at work here, including conservation of momentum,application of force, levers, and much more. But for now, consider the physics of the fate of the dunked subject. From the thermodynamics of this system, we can see that the dunked individual cools with each cycle. Describe the ultimate temperature of the dunked individual over time.

Assumptions:

● The throwers are spot on and the timing is such that the dunked person is out of the water for the same amount of time as they are in the water.
● The in-and-out cycle happens at a regular interval.
● The time to crawl out of the tank and resume the position on the chair is negligible, i.e., we can consider only submerged time and unsubmerged time.
● It’s a sunny, warm day, about 85 ºF, and the water has reached equilibrium with the temperature of the surrounding air.
● The surrounding air is moving with some reasonable breeze speeds. (This influences the cooling rate of the wet individual during the out-of-water time.)

The Joule (or watt-second) replaced the erg as the accepted unit of both magnetic and mechanical energy. The unit is named after James Prescott Joule (1818-1889).

References:
1. Environmental Protection Agency , Average Temperature of Shallow Ground Water, Accessed Nov. 17, 2019, www3.epa.gov/ceampubl/learn2model/part-two/onsite/ex/jne_henrys_map.html .
2. NIST Chemistry WebBook, Accessed Nov. 17, 2019, webbook.nist.gov/.
3. Khan Academy – Evaporative Cooling, www.khanacademy.org/science/biology/water-acids-and-bases/water-as-a-solid-liquid-and-gas/v/evaporative-cooling .
4. We got about 7000 kJ.
5. A. Guyton and J. Hall, Textbook of Medical Physiology, 12th ed. (W. B. Saunders Co., Philadelphia, 2010).
6. Osborne, N., Stimson, H., and Ginnings, D., Measurement of Heat Capacity and Heat of Vaporization of Water in the Range of 0 to 100 C, J. Res. Natl. Bur. Stand., Vol. 23, Paper No. Rp1228 (Aug. 1939), https://nvlpubs.nist.gov/nistpubs/jres/23/jresv23n2p197_A1b.pdf .