Physics Puzzler: Does Ideal Baseball Mean No Air Resistance?!
As most readers well know, in introductory physics we talk ad nauseum about projectile motion. It’s a never-ending stream of firing cannon balls straight up, throwing rocks at arbitrary angles, and even watching the occasional space ship move in all kinds of strange ways. Luckily, at least in first-year physics courses, we get to start the discussion with the heartwarming phrase “assuming no air resistance . . . .” 1 Those four words make things so much easier.
As we thaw into spring in the Northern Hemisphere, many countries welcome the beginning of baseball season (which is super different from cricket but still involves a bat and ball), and this got me thinking. If baseball existed in an ideal world, would this lead to a totally different game? Or would we hardly notice a difference? Let’s find out.
To start things off, if there was no air resistance, how much larger would we need to make baseball fields?
There are many ways to look at this, but a little background first.
1) In baseball, one player throws a ball really fast at a person with a wooden bat. These pitched balls can reach speeds in excess of 150 km/hr! The fastest recorded pitch was about 166 km/hr.2
2) As you might imagine, a baseball field is very well defined in the game rules. It needs to be flat with 90 ft (27.4 m) between the diamond bases and separated from fences by a minimum distance of 290 ft (97 m) and 400 ft (133 m), as shown in my crude drawing, see Fig. 2. If a ball is hit over the fence, it’s a home run!
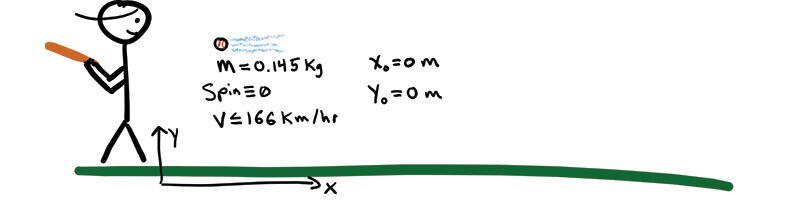
Official baseballs can have a mass variance of ½ ounce (14 g) and a radius variance of ¼ inch (6 mm)—so there is significant variance). All images by the author.

A crude illustration of a baseball diamond and the distance to the back fence, which marks a home run. The farthest home run ever hit (and properly measured) was roughly 582 ft.
Using these numbers, we can address the question of how large to make a baseball field with no air resistance. I think it’s fair to assume that if a player hits a standard fast ball perfectly, at a 45° angle, it should land at the back fence. So, in my ideal baseball game, how far would that perfectly hit ball go?
From kinematics and being extra careful with units, we get 178 m (or 583 ft), which is substantially longer than a standard field—about 45% longer. This means air resistance has a huge impact on baseball. If we kept the field the same, baseballs hit at a wide variance in angle would be home runs, driving up the scores A LOT! If we wanted to keep the scoring roughly the same, we’d need to move the back fence 44 m farther out (145 ft). And to carry the calculation through, if we hit the fastest baseball ever recorded it would travel 217 m (or 711 ft).

A handwritten solution for a baseball hit in a vacuum using kinematics.

A sketch comparing the projectile motion curves for a home run (blue) and the ideal case (orange).
Notes:
1. I say “heartwarming” because anytime I can avoid a complicated differential equation, my students say it’s a good day.
2. Robert K. Adair, The Physics of Baseball, 3rd ed., Revised, Updated, and Expanded (New York: Harper & Row, 2002).
3. See either Robert K. Adair’s book, or “The Effect of Air on Baseball Pitches,” the webpage of Michael Richmond, accessed March 6, 2022, spiff.rit.edu/richmond/baseball/traj/traj.html
This leads to this issue’s puzzler! Given the information in this article and anything you can estimate, consider this:
Often a ball will be hit to the fence and passed toward home plate. If the outfield fence was, in fact, 183 feet farther out and a batter hit a ground ball all the way to the fence, how much extra time would it give a player to run around the baseball diamond to try and score? Would we even notice the time difference?
And if you are looking for an additional challenge, you can examine the relative effects of air drag and ball spin.3 I challenge you to examine whether ball spin increases or decreases how far a hit ball will travel.
If you would like to share your work and answers on social media, please tag @SPSNational and we will repost you! //



